数学専門プロ家庭教師による授業についてのご説明です。
「Zoom」を利用し、生徒と教師の対話による双方向授業が全国で受講可能です。
対象とする方
数学に不安のある大学受験生(高校生、浪人生)が主な対象です。
その他、大学生、中学生も対象としています。
- 数学の偏差値が30~40台
- 中学数学から復習したい
- 参考書を一人で読み進めることができない
- 週に複数回の授業で勉強習慣を見に付けたい
個人契約の家庭教師ですので、お問い合わせの段階から教師自身が直接対応し、
生徒さん一人ひとりに対応したオーダーメイド型授業をオンラインで提供します。
成績を伸ばす対話型の個別指導
私の個別指導のやり方を説明する前に、まず一般的な指導方法をみてみましょう。
教師の説明は読み飛ばして頂いても大丈夫です。
一般的な数学教師のよくある指導例

x² - 6x + 5 < 0 の整数解の個数を求めてみよう。

う~ん。わかりません。

最初にやるべきことは、因数分解だよ。
x² - 6x + 5 = (x - 1)(x - 5) って因数分解できるね。
だから、不等式は (x−1)(x−5)<0 になるんだ。
次に、これを数直線で考えるよ。
ポイントは、x = 1 と x = 5 の2つの値で区切ることだよ。この2つの値が境界になるんだね。
まず、x が 1 より小さいとき(たとえば x = 0 のとき)どうなるか見てみよう。
このとき、(0−1)(0−5)だから、正の数になるよね。
だからこの範囲では不等式は成り立たない。
次に、x が 1 より大きくて 5 より小さいとき(たとえば x = 3 のとき)を考えるよ。
(3−1)(3−5)だから、負の数になる。
つまり、この区間では不等式が成り立つんだ。
最後に、x が 5 より大きいとき(たとえば x = 6)も見てみるよ。
(6−1)(6−5) だから、また正の数になるね。
だからこの範囲も不等式は成り立たない。
だから、不等式が成り立つのは 1 < x < 5 の間ってことだね。
あとはこの範囲に含まれる整数を見てみよう。
x = 2, 3, 4 の3つが該当するね。
これで、この不等式の整数解は 3つ だってわかるよ!
この解説はちゃんと送るから安心して!

わかりました。

何か質問はあるかな?

いえ、大丈夫です。
解説直後は生徒さんはわかったと納得しています。
また、最後に質問はないかと聞いていますが、生徒さんは大丈夫と答えています。
解説も丁寧ですし、質問も聞いてくれるしいい先生のようにみえます。
ただ、問題を一気に解説しているので、生徒さんは自分の手は全く動いていませんね。
私が大切にしている指導例
一般的な数学家庭教師の先生と違い、私の授業では頻繁に会話のキャチボールをして、生徒さんが手を動かせるようにしています。

x² - 6x + 5 < 0 の整数解の個数を求めてみよう。

う~ん、わかりません。

じゃあまず左辺の二次式をグラフにしてみましょうか。

え~と、グラフってどうやるんでしたっけ。

では左辺の二次式を因数分解してみたらどうでしょうか。

それはできそう。はい因数分解できました。(x - 5)(x - 1) ですね。

ばっちりです!

あ、てことは二次式のグラフも描けそう。こうですか?
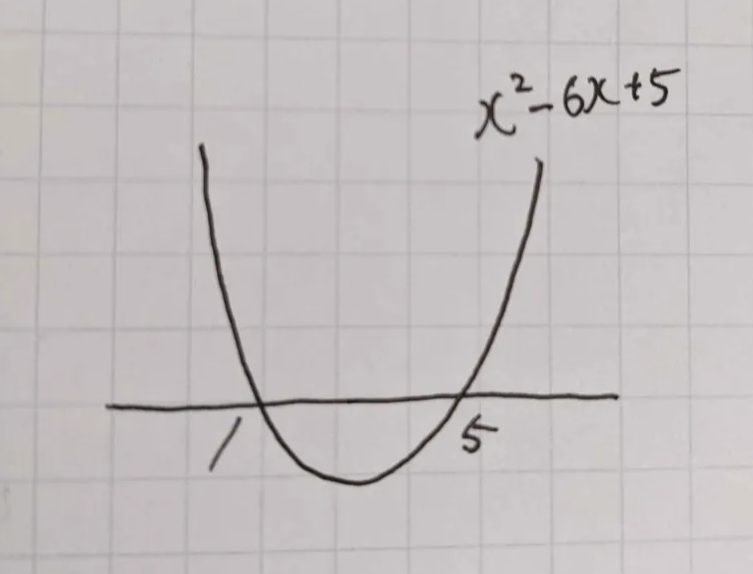

素晴らしい!このグラフで0未満のところが解ということですね。では解xの満たす範囲を不等式で書いてみましょう。

え~と、このグラフのこの部分だから、1 < x < 5かな。ということは含まれる整数解は4個ですね。
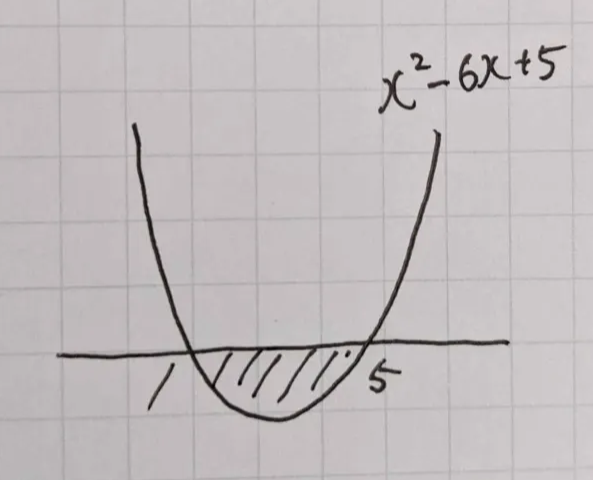

惜しいです!不等式の1 < x < 5を数直線上で描いてみたらどうでしょうか?

(数直線を描いて)あ、整数は3個ですね。端っこの2つは含まれないですもんね。
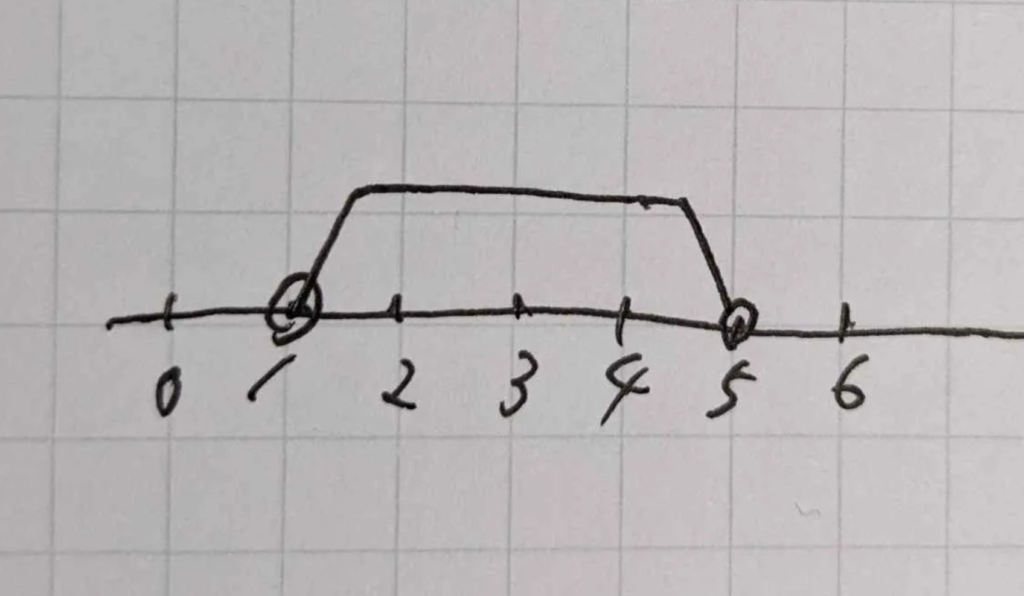

そのとおり、正解です!できましたね。

数直線にして図解したらわかりました。

そうなんですよ!面倒でも頭のなかで済ませようとせず、どんどん描き出しましょう!
私の授業では生徒さんと何度も会話を往復し、生徒さんがたくさん図や式を描いています。
(もちろん解説が必要なところは私もたくさん図や式をかきます)
基本問題であっても、数学は論点がたくさんあるんですね。
そして生徒さんは問題がわからないといっても、全部の論点がわからないということはありません。
生徒さんができるところは自分で描きながら考え、躓いたら助け舟を出す、これが基本です。
ですから基本問題でもこうやって何度も会話を往復しながら、たくさん図と式を描きながら進みます。
復習のとき、同じ問題を自力で最後まで解けるか?
一般的な授業スタイルで解説を聞いただけの生徒さんは、
復習の際に自力で問題を解けないことの方が多いです。
そして「解説を聞いたのに…やっぱり自分数学のセンスがないんだ…」と落ち込んでしまうことがあります。
しかし、私の授業を受けた生徒さんの場合は、
復習の際に自力で解けることがずっと多くなります。
「数学体験」の差が上達を分ける
私の授業では対話によって、
生徒さんは何度も自分で考え、図や式を自分の手で描いています。
その過程で間違えたら、自分で考えを修正します。
わたしはこれを「数学体験」と呼んでいます。
一方、先生が問題を一度に解説する一般的なスタイルは、
生徒は自分で図も式も描かないし、自分で間違ってもいません。
つまり「数学体験」がまったくない状態です。
この「数学体験」の差が、復習のときに自力で問題を解けるかの差になっています。
それが積み重なって数学の実力の差になっていきます。
オンライン数学家庭教師(短期指導)
短期の指導もご相談ください。
- 夏休み・冬休み等の長期休暇
- 全寮制中学・高校から自宅へ戻った際
- 定期テスト前
- 普段の学校や塾と違う教え方の授業を受けたい(セカンドオピニオン)
- 参考書や問題集の選び方、勉強の仕方を知りたい生徒さん
ご依頼が良くある短期例
- 数学の基礎を短期・集中的に受けたい→ 短期数学基礎集中講座
- 期末・中間テスト前だけ指導を受けたい→ 定期テスト対策
- 数学の家庭教師が緊急に必要な方
個人契約の家庭教師のため、急なご依頼にも可能な限り素早く、オンラインで対応ができます。例えば、以下のような場合にも対応可能です:- 数学の追試数学課題が急に出された
オンライン家庭教師 体験授業について
初回の授業は「体験授業(無料)」となり、オンラインで受講が可能です。
